
Exercise 6ĭetermine if the following function is continuous.
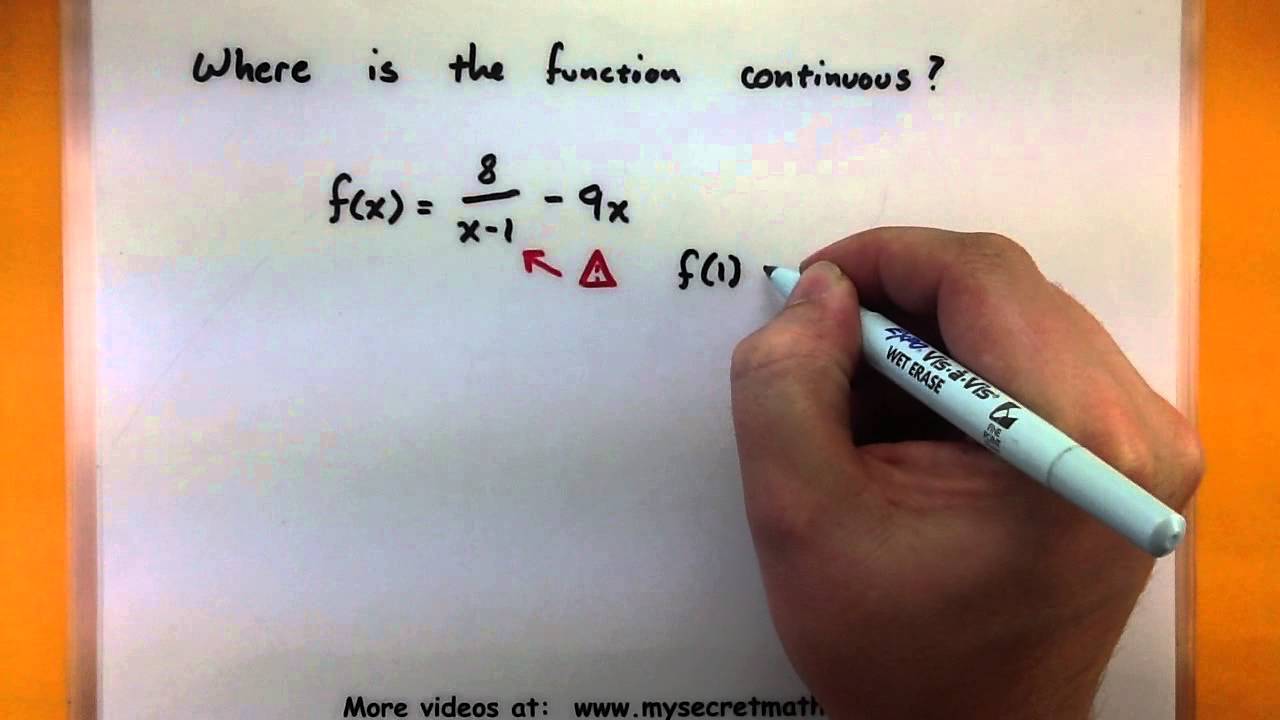
If not, state where the discontinuities exist and what type they are:Īre the following functions continuous at x = 0?ġ Prove that f(x) is not continuous at x = 5.ĢIs there a continuous function which coincides with f(x) for all values with the exception x = 5? If so, determine the function. Loosely and informally written, a function is continuous if there is no sudden jump in its graph, but rather the graph is connected.Ī function is said to be discontinuous at a value a if there is a jump in the graph at a.Determine if the following function is continuous at x = 0.ĭetermine if the following function is continuous on (0,3). In calculus, we typically assume that the functions we work with are continuous.

Continuous Functionsįunctions can have a wide range of different properties. f: ℝ→ℝ defined by f(x)=2x, where ℝ is the set of real numbers.

Sometimes we write the rule that the function applies explicitly e.g. If we denote the domain of a function f by A and the codomain of f by B, then we usually denote that more concisely by f: A → B. You should think of f as a rule that takes an element from the domain and outputs one and only one element from the codomain. We won’t go into a set-theoretic definition of functions, instead, we shall think of them from a higher and more intuitive level.Ī function f has two important sets associated with it. Therefore, it makes sense to make sure that we understand functions properly before moving on.
#Continuity calculus free#
We won’t, however, be totally free of complex numbers because they will play an important role later, but I will introduce you to them when we get there. In this series, if nothing else stated, I will assume that the functions are real, that is, from subsets of the real numbers to the real numbers.Ĭomplex calculus (called complex analysis) is an entirely different beast. In calculus, we typically study the functions of real or complex numbers. In other words: if x is an element in A then x is an element in B. That a set A contains an element a is written a ∈ A.Ī subset A of a set B is written A ⊂ B and it simply means that for all x we have x ∈ A => x ∈ B. We can also have sets of vectors, functions, points, etc. Examples of sets include number sets like the whole numbers, real numbers, and finite sets such as the set containing the numbers 1, 2, and 3. What a set truly is, is a long story, so for us, it will suffice to think of sets (naively) as collections of elements. In mathematics, sets are special objects that are quite fundamental to all mathematics. But as always, you do need to know what is really happening under the hood so to speak. If you ask the right questions, you will be guided through the arguments until you arrive at the solution. You almost get a magical feeling, when solving problems with calculus. Then I learned about derivatives, and I was immediately interested.Ĭalculus is very useful and can solve problems that we just can’t solve without it.

But I had enough of simple equations and reductions. When I first studied it, I remember feeling excited because up until then I felt like the whole subject of mathematics was quite boring (obviously I hadn’t got the first clue as to what mathematics really is). Calculus may seem intimidating for some because it signifies a leap in mathematical maturity from basic algebra and arithmetic to function theory, however, it is actually a beautiful, useful, and not so hard subject if one takes the time to understand the very basics of it first.


 0 kommentar(er)
0 kommentar(er)
